Go 语言实现 Redis 跳表

发表于 | 分类于
| 字数统计: 2.5k | 阅读时长 ≈ 10

引言


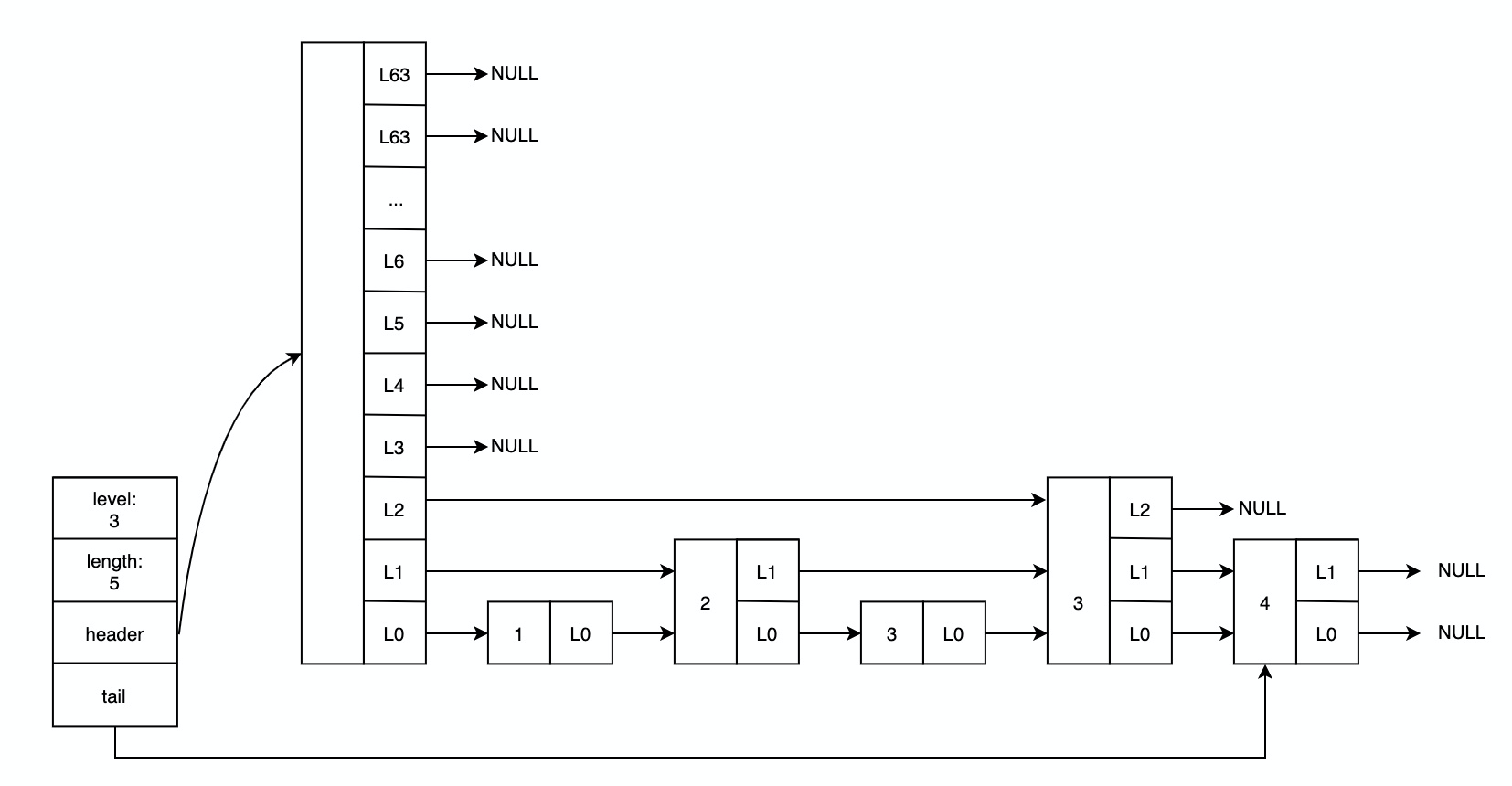
读过 Redis 源码的童鞋，想必会知道 zset 实现时，使用了「跳表」（Skiplist）这种数据结构吧。它的原理非常容易理解，如果对链表比较熟悉，那么也会很容易理解「跳表」的工作原理（核心：有序链表 + 分层）。当然，本文并不会详细讲解「跳表」的工作原理，以及对于 Redis 跳表源码的详细分析。因为已经有前辈们产出了非常丰富的文章来讲解 Redis 跳表，需要的话，推荐阅读 这篇文章 了解更多细节。

总的来说，Redis 的 zset 实现中，选用「跳表」的主要原因如下：

  1. 原理清晰易懂，且容易实现，方便维护：对比下平衡树或者红黑树（可能就像 Raft v.s. Paxos 的感觉一样），不管是原理还是实现都简单了很多。平衡树或者红黑树在实现时，还要时刻维护节点关系，必要时还需要执行树的左旋或者右旋来保持平衡；
  2. 拥有媲美平衡树或者红黑树的查询效率：插入、删除、查找的平均时间复杂度可以达到 O(logN)。

当然，相对于 William Pugh 在他的论文中所描述的「跳表」算法而言，作者在实现 Redis 中的「跳表」时，给它加了点「料」：

  1. 允许重复的分数存在；
  2. 在进行比较时，不仅会比较 score，还会考虑关联的数据；
  3. 添加了一个回退指针，从而构成了一个双向链表（level[0]），便于倒序遍历链表（ZREVRANGE）使用。

好了，废话完毕。接下来进入正题，看看如何使用 Go 语言来实现「跳表」吧（贴代码模式开启~）。

跳表实现

以下仅仅列出了几个比较有趣且关键的方法实现，即：插入、删除和更新分数。完整的实现源码可以参考 这里 或者 这里，包含了比较详细的单元测试。

数据结构定义

需要说明的是，为了简单起见，假设存储的元素是字符串类型（要是使用 interface{} 的话，又得加些代码支持元素之间的比较了）。但是在 Redis 中，实际的 element 类型是 sds。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
const (
    MaxLevel = 64 // 足以容纳 2^64 个元素
    P = 0.25
)

type Node struct {
    elem string
    score float64
    backward *Node
    level []skipLevel
}

type skipLevel struct {
    // forward 每层都要有指向下一个节点的指针
    forward *Node
    // span 间隔定义为：从当前节点到 forward 指向的下个节点之间间隔的节点数
    span int
}

type Skiplist struct {
    header, tail *Node
    level int // 记录跳表的实际高度
    length int // 记录跳表的长度（不含头节点）
}

辅助方法

考虑到在实现时，经常需要比较 score 和 element，所以这里直接给 Node 实现了一些比较方法，便于使用。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
func (node *Node) Compare(other *Node) int {
    if node.score < other.score || (node.score == other.score && node.elem < other.elem) {
        return -1
    } else if node.score > other.score || (node.score == other.score && node.elem > other.elem) {
        return 1
    } else {
        return 0
    }
}

func (node *Node) Lt(other *Node) bool {
    return node.Compare(other) < 0
}

func (node *Node) Lte(other *Node) bool {
    return node.Compare(other) <= 0
}

func (node *Node) Gt(other *Node) bool {
    return node.Compare(other) > 0
}

func (node *Node) Eq(other *Node) bool {
    return node.Compare(other) == 0
}

插入元素

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
// Insert 向跳表中插入一个新的元素。
// 步骤：
// 1. 查找插入位置
// 2. 创建新节点，并在目标位置插入节点
// 3. 调整跳表 backward 指针等
func (sl *Skiplist) Insert(score float64, elem string) *Node {
    var (
        // update 用于记录每层待更新的节点
        update [MaxLevel]*Node
        // rank 用来记录每层经过的节点记录（可以看成到头节点的距离）
        rank [MaxLevel]int
        // 构建一个新节点，用于下面的大小判断，其 level 在后面设置
        node = &Node{score: score, elem: elem}
    )
    cur := sl.header
    for i := sl.level - 1; i >= 0; i-- {
        if cur == sl.header {
            rank[i] = 0
        } else {
            rank[i] = rank[i+1]
        }
        // 与同层的后一个节点比较，如果后一个比目标值小，则可以继续向后
        // 否则下降到一层查找。注意这里的大小比较是按照 score 和
        // elem 综合计算得到的。
        for cur.level[i].forward != nil && cur.level[i].forward.Lt(node) {
            rank[i] += cur.level[i].span
            // 同层继续往后查找
            cur = cur.level[i].forward
        }
        update[i] = cur
    }
    // 调整跳表高度
    level := sl.randomLevel()
    if level > sl.level {
        // 初始化每层
        for i := level - 1; i >= sl.level; i-- {
            rank[i] = 0
            update[i] = sl.header
            update[i].level[i].span = sl.length
        }
        sl.level = level
    }
    // 更新节点 level，并插入新节点
    node.setLevel(level)
    for i := 0; i < level; i++ {
        // 更新每层的节点指向
        node.level[i].forward = update[i].level[i].forward
        update[i].level[i].forward = node
        // 更新 span 信息
        node.level[i].span = update[i].level[i].span - (rank[0] - rank[i])
        update[i].level[i].span = (rank[0] - rank[i]) + 1
    }
    // 针对新增节点 level < sl.level 的情况，需要更新上面没有扫到的层 span
    for i := level; i < sl.level; i++ {
        update[i].level[i].span++
    }
    // 调整 backward 指针
    // 如果前一个节点是头节点，则 backward 为 nil
    // 否则 backward 指向之前节点
    if update[0] != sl.header {
        // update[0] 就是和新增节点相邻的前一个节点
        node.backward = update[0]
    }
    // 如果新增节点是最后一个，则需要更新 tail 指针
    if node.level[0].forward == nil {
        sl.tail = node
    } else {
        // 中间节点，需要更新后一个节点的回退指针
        node.level[0].forward.backward = node
    }
    sl.length++
    return node
}

// randomLevel 对于新增节点，返回一个随机的 level
// 返回的 level 范围为 [1, MaxLevel]。并且，采用的
// 算法会保证，更大的 level 返回的概率越低。
// 每个 level 出现的概率计算：(1-p) * p^(level-1)
func (sl *Skiplist) randomLevel() int {
    level := 1
    for rand.Float64() < P && level < MaxLevel {
        level++
    }
    return level
}

删除元素

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
// Delete 用于删除跳表中指定的节点。
func (sl *Skiplist) Delete(score float64, elem string) *Node {
    // 第一步，找到需要删除节点
    var (
        update [MaxLevel]*Node
        targetNode = &Node{elem: elem, score: score}
    )
    cur := sl.header
    for i := sl.level - 1; i >= 0; i-- {
        for cur.level[i].forward != nil && cur.level[i].forward.Lt(targetNode) {
            cur = cur.level[i].forward
        }
        update[i] = cur
    }
    // 目标节点找到后，这里需要判断下 elem 是否相等
    // score 可以重复，所以必须要谨慎
    nodeToBeDeleted := update[0].level[0].forward
    if nodeToBeDeleted == nil || !nodeToBeDeleted.Eq(targetNode) {
        return nil
    }
    sl.deleteNode(update, nodeToBeDeleted)
    return nodeToBeDeleted
}

func (sl *Skiplist) deleteNode(update [64]*Node, nodeToBeDeleted *Node) {
    // 这时我们要删除的节点就是 nodeToBeDeleted
    // 调整每层待更新节点，修改 forward 指向
    for i := 0; i < sl.level; i++ {
        if update[i].level[i].forward == nodeToBeDeleted {
            update[i].level[i].forward = nodeToBeDeleted.level[i].forward
            update[i].level[i].span += nodeToBeDeleted.level[i].span - 1
        } else {
            update[i].level[i].span--
        }
    }
    // 调整回退指针：
    // 1. 如果被删除的节点是最后一个节点，需要更新 sl.tail
    // 2. 如果被删除的节点位于中间，则直接更新后一个节点 backward 即可
    if sl.tail == nodeToBeDeleted {
        sl.tail = nodeToBeDeleted.backward
    } else {
        nodeToBeDeleted.level[0].forward.backward = nodeToBeDeleted.backward
    }
    // 调整层数
    for sl.header.level[sl.level-1].forward == nil {
        sl.level--
    }
    // 减少节点计数
    sl.length--
    nodeToBeDeleted.backward = nil
    nodeToBeDeleted.level[0].forward = nil
}

更新分数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
// UpdateScore 用于更新节点的分数。该函数会保证更新分数后，
// 节点的有序性依然可以维持。
// 策略如下：
// 1. 快速判断能否原节点修改，如果可以则直接修改并返回；
// 2. 采用更加昂贵的操作：删除再添加。
func (sl *Skiplist) UpdateScore(curScore float64, elem string, newScore float64) *Node {
    var (
        update [MaxLevel]*Node
        targetNode = &Node{elem: elem, score: curScore}
    )
    cur := sl.header
    // 第一步，找到符合条件的目标节点
    for i := sl.level - 1; i >= 0; i-- {
        for cur.level[i].forward != nil && cur.level[i].forward.Lt(targetNode) {
            cur = cur.level[i].forward
        }
        update[i] = cur
    }
    node := cur.level[0].forward
    if node == nil || !node.Eq(targetNode) {
        return nil
    }
    if sl.canUpdateScoreFor(node, newScore) {
        node.score = newScore
        return node
    } else {
        // 需要删除旧节点，增加新节点
        sl.deleteNode(update, node)
        return sl.Insert(newScore, node.elem)
    }
}

// canUpdateScoreFor 确定能否直接在原有的节点上进行修改
// 什么条件才可以直接原地更新 score 呢？
// 1. node 是唯一一个数据节点（node.backward == NULL && node->level[0].forward == NULL）
// 2. node 是第一个数据节点，且新的分数要比 node 之后节点分数要小（这样才能保证有序）
// 即：node.backward == NULL && node->level[0].forward->score > newScore）
// 3. node 是最后一个数据节点，且 node 之前节点的分数要比新改的分数小
// 即：node->backward->score < newScore && node->level[0].forward == NULL
// 4. node 是修改的后的分数恰好还能保证位于前一个和后一个节点分数之间
// 即：node->backward->score < newscore && node->level[0].forward->score > newscore
func (sl *Skiplist) canUpdateScoreFor(node *Node, newScore float64) bool {
    if (node.backward == nil || node.backward.score < newScore) &&
        (node.level[0].forward == nil || node.level[0].forward.score > newScore) {
        return true
    }

    return false
}

总结

俗话说，「说起来容易，做起来难」。在实现「跳表」的时候感受颇深，似乎看完 Redis 的「跳表」源码和网上诸多前辈编写的文章后，自以为懂得了原理（可能确实懂了），但是在具体实现的时候还是踩了不少坑。比如，空指针引起 panic；i-- 写成了 i++ 导致查找失败；一些边界情况的判断等。总之，细节决定成败，需要在保持思路清晰的同时，更加谨慎一些才能写出足够健壮的代码来。当然，这期间自然少不了单元测试的助攻，否则有很多问题可能都没法暴露出来~

参考

0%